Cómo estimar parámetros en un modelo por máxima verosimilitud (versión fuerza bruta)

Una parte importante de los modelos estadísticos es la forma en la que se estiman los parámetros. En modelos lineales (regresión, ANOVA, ANCOVA), la estimación se hace frecuentemente por el método de mínimos cuadrados. En modelos lineales generalizados (GLM) la estimación se hace por el método de máxima verosimilitud. Cómo opera este método es algo normalmente desconocido al usuario estándar de programas estadísticos (incluido R). Aunque hay muchas formas de estimar los parámetros de un modelo utilizando máxima verosimilitud, la idea subyacente es la misma: encontrar los parámetros que maximizan la probabilidad de los datos observados. La forma más intuitiva de hacer esta estimación es por fuerza bruta, esto es, probando muchas posibles combinaciones de los valores de los parámetros y ver qué combinación maximiza la probabilidad de los datos. A continuación pongo un breve manual sóbre cómo hacer esto en R con objeto de poder entender un poco mejor este proceso. 

Cómo estimar los parámetros de un modelo por máxima verosimilitud en R

No obstante, esta forma iterativa es computacionalmente inpracticable, como se explica en el manual, y distintos métodos se han ideado para solucionar estos problemas y encontrar parámetros óptimos (locales y globales). No entraré a detallar los distintos métodos de estimación por máxima verosimilitud, pero si entendemos la idea de fondo, creo que será mucho más fácil entender el proceso por el que generamos nuestros modelos y algunos de los problemas (por ejemplo, convergencia) que a veces surgen por el camino.

Modelos a la carta: El modelo gaussiano

Los modelos lineales generalizados (GLM) tienen tres componentes: (1) la estructura de errores; (2) el estimador lineal y; (3) la función de vínculo. La función de vínculo linealiza la relación entre la respuesta y el estimador lineal. La función de vínculo, junto con el estimador lineal, constituyen lo que lo algunos autores denominan el "modelo científico". La máxima versatilidad en la modelización se alcanza cuando uno ajusta modelos a la carta, fuera de las restricciones que los GLM imponen. Ello implica que debemos escribir nuestras propias funciones, para después ajustarlas a los datos. El proceso se completa en el contexto de la selección de modelos por criterios de información cuando comparamos toda una batería de modelos plausibles ajustados por métodos de máxima verosimilitud. En R esto puede hacerse por medio del paquete 'likelihood' escrito por Lora Murphy. El paquete todavía no está disponible en CRAN, aunque es de esperar que lo esté pronto. Mientras tanto, este paquete se puede descargar de la página del curso de "Modelos y métodos de máxima verosimilitud" de Charlie Canham. Este curso fue por cierto impartido en abril en Granada y he de decir que ha sido uno de los mejores cursos a los que he asistido... ¡gracias Charlie!

Bueno, a lo que iba... en lo que respecta a los modelos científicos. Podemos usar muchos tipos de modelos dependiendo de los datos que tengamos. No tienen por qué ser lineales. Una familia de modelos muy versátiles que permiten ajustar respuestas que aumentan primero y disminuyen después son los modelos gaussianos. La función gaussiana se expresa así:

$y=a\cdot e^{(\frac{-{(X-b)}^2}{(2\cdot c^2)})}$

Dicha función consta de 3 parámetros, que llamaremos 'a', 'b' y 'c', pero que podríamos haber denominado de cualquier otra forma. El parámetro 'a' indica el valor máximo que alcanza la curva. El parámetro 'b' determina la forma de la curva: monotónica, creciente, decreciente. El parámetro 'c' va a condicionar la pendiente de la curva (lo que en inglés se denomina sharpness).

Veamos ahora cómo cambios en los valores de estos parámetros determinan cambios en la forma de las curvas tipo. Tomemos un ejemplo en dónde vamos a modelar la abundancia de arácnidos en sistemas agrícolas (y) en función del tiempo (X). La idea con el siguiente código en R es que nos familiaricemos con esta función y sus parámetros.

Si modificamos el parámetro 'a' podemos obtener algunas las siguientes curvas:

X <- 1:250
a <- 1000
b <- 125
c <- 0.01
Y1 <- a*exp(-((X-b)^2/2*c^2))
plot(Y1~X, type="l", ylim=c(0,1050), ylab="Abundancia de arácnidos", xlab="Tiempo", main="Función gausiana")
text(x=125, y=1025, "a=1000")
a <- 800
Y1 <- a*exp(-((X-b)^2/2*c^2))
lines(X, Y1, lty=2)
text(x=125, y=825, "a=800")
a <- 600
Y1 <- a*exp(-((X-b)^2/2*c^2))
lines(X, Y1, lty=3)
text(x=125, y=625, "a=600")
a <- 400
Y1 <- a*exp(-((X-b)^2/2*c^2))
lines(X, Y1, lty=4)
text(x=125, y=425, "a=400")
a <- 200
Y1 <- a*exp(-((X-b)^2/2*c^2))
lines(X, Y1, lty=5)
text(x=125, y=225, "a=200")

Modificando el parámetro 'b' obtenemos cambios en la forma de la curva gaussiana como se observa en la siguiente gráfica:

X <- 1:250
a <- 1000
b <- 125
c <- 0.01
Y1 <- a*exp(-((X-b)^2/2*c^2))
plot(Y1~X, type="l", ylim=c(0,1050), ylab="Abundancia de arácnidos", xlab="Tiempo", main="Función gausiana")
text(x=125, y=1025, "b=125")
b <- 200
Y1 <- a*exp(-((X-b)^2/2*c^2))
lines(X, Y1, lty=2)
text(x=200, y=1025, "b=200")
b <- 275
Y1 <- a*exp(-((X-b)^2/2*c^2))
lines(X, Y1, lty=4)
text(x=240, y=825, "b=275")
b <- 50
Y1 <- a*exp(-((X-b)^2/2*c^2))
lines(X, Y1, lty=5)
text(x=50, y=1025, "b=50")
b <- -25
Y1 <- a*exp(-((X-b)^2/2*c^2))
lines(X, Y1, lty=5)
text(x=15, y=825, "b=-25")

Cambios en el parámetro 'c' van a provocar cambios en las pendientes de la curva, como se observa a continuación:

X <- 1:250
a <- 1000
b <- 125
c <- 0.01
Y1 <- a*exp(-((X-b)^2/2*c^2))
plot(Y1~X, type="l", ylim=c(0,1050), ylab="Abundancia de arácnidos", xlab="Tiempo", main="Función gausiana")
text(x=45, y=825, "c=0.01")
c <- 0.001
Y1 <- a*exp(-((X-b)^2/2*c^2))
lines(X, Y1, lty=2)
text(x=125, y=1025, "c=0.001")
c <- 0.25
Y1 <- a*exp(-((X-b)^2/2*c^2))
lines(X, Y1, lty=4)
text(x=125, y=150, "c=.025")
c <- 0.1
Y1 <- a*exp(-((X-b)^2/2*c^2))
lines(X, Y1, lty=5)
text(x=90, y=250, "c=0.1")
c <- 0.02
Y1 <- a*exp(-((X-b)^2/2*c^2))
lines(X, Y1, lty=5)
text(x=40, y=400, "c=0.02")

Mayor riesgo de infección alimentaria por E. coli en ganado alimentado con grano

Aunque Escherichia coli es un organismo comensal que reside dentro del intestino del huésped, algunas cepas patógenas de E. coli pueden causar colitis hemorrágica en humanos. Una de las cepas más infecciosas de E. coli es la O157:H7. El ganado es un reservorio asintomático de esta cepa. Esto quiere decir que contiene la cepa, pero que ésta no produce síntomas de la enfermedad. Normalmente la cepa está presente en alrededor de un 30% del ganado y, en determinadas ocasiones, puede llegar a estar presente en hasta el 80% del del ganado.

 
Al ganado intensivo, ya sea en su aptitud productiva de carne o leche, se le alimenta frecuentemente con grano (cereales y leguminosas) con el objeto de aumentar la eficiencia alimentaria, ya que el grano contiene muchas más calorías que el pasto en forma de hidratos de carbono, fundamentalmente almidón. Cuando el ganado es alimentado con mucho grano, algo de almidón escapa a la degradación microbiana del rúmen y pasa al intestino, donde es fermentado. E. coli O157:H7 fermenta los azúcares que se liberan tras la ruptura del almidón en el colon. Esto implica que tiene alimento suficiente para reproducirse y aumentar sus poblaciones, por lo que aparece en mayores densidades en esta parte del aparato digestivo, lo que se traduce finalmente en una mayor presencia de esta cepa en las heces.

El ganado intensivo se hacina en pequeñas concentraciones parcelarias, dónde la acumulación deheces es alta. Como consecuencia de ello, se han producido intoxicaciones de E. coli O157:H7 en reses sacrificadas procedentes de dichas explotaciones. La contaminación se produce por el contacto exterior de los animales con las heces. Aunque en los mataderos hay sistemas de limpieza y desinfección, cuanto mayor sea la proporción de E. coli, mayor será el riesgo de fallo de estos sistemas y ésta acabará entrando en contacto con la carne procesada tras el sacrificio.

Otra forma de intoxicación se produce cuando se utilizan estas heces como abono, como ocurrió recientemente en la famosa crisis del pepino (aunque la cepa aquí era otra). En este caso la intoxicación se produce a través de alimentos de origen vegetal, aunque este tipo de intoxicaciones son más raras.

¿Qué se puede hacer? No es necesario hablar de sistemas alternativos a los sistemas de explotación ganaderos intensivos. Pero sin necesidad de movernos hacia posturas totalmente contrarias, una revisión no ya tan reciente (Callaway et al. 2003) demuestra que basta con que el ganado sea alimentado 5 días con pasto para que las poblaciones de E. coli en el colon disminuyan del orden de 1000 veces su densidad, y que la capacidad de las poblaciones de E. coli para sobrevivir a los ácidos gástricos del estómago humano descienda drásticamente.

Por supuesto que también es necesario aumentar los controles sanitarios en explotaciones intensivas para evitar este tipo de problemas.

Callaway TR, Elder RO, Keen JE, Anderson RC, & Nisbet DJ (2003). Forage feeding to reduce preharvest Escherichia coli populations in cattle, a review. Journal of dairy science, 86 (3), 852-60 PMID: 12703622

Niños delante del televisor: ¿qué hacemos los padres para potenciarlo?

Como padre en ejercicio me he sentido muy identificado con la lectura de un artículo de investigación recientemente publicado en la revista Public Health Nutrition titulado “Parental factors associated with screen time in pre-school children in primary-care practice: a TARGet Kids! Study”. Se trata de un estudio realizado en Toronto, Canadá, con una población muestral de niños de 3 años. Se entrevistaba a los padres y se recogían datos de la cantidad de tiempo que los niños pasaban delante del televisor diariamente, además de información relacionada con las condiciones socio-económicas, culturales y laborales de los padres. El estudio pone en evidencia una relación positiva entre tiempo de exposición a la televión y el hábito de comer viendo la tele, madres trabajadoras, y padres que pasan más tiempo delante de la tele. También detectó una relación negativa entre tiempo de exposición a la tele y la existencia de normas en la casa con respecto a cuándo se puede ver y no ver la tele.

En conclusión, como padres, además de tener que predicar con el ejemplo sobre el consumo moderado de programas televisivos, tenemos que poner algunas normas a nuestros hijos para que sepan que la tele no es un entretenimiento al que puedan recurrir a cada rato. En cualquiera de los casos, hay que saber que la televisión en niños menores de 3 años tiene siempre efectos negativos, a saber: retrasa el desarrollo del lenguaje, genera comportamientos agresivos, sobrepeso y obesidad (los niños delante de la tele no se dan cuenta de qué están comiendo y comen, por lo general, por encima de sus necesidades). La propia Sociedad Canadiense de Pediatría recomienda que los niños de pre-escolar (menores de 3 años) no vean la tele más de 1 hora diaría. No sé que dirá la Asociación Española de Pediatría. En un vistazo rápido no he encontrado nada en su página web, pero sí he encontrado algunos artículos más de investigaciones españolas que alertan del uso y abuso de la televisión.

Así que ¡tomemos nota y tengamos cuidado sobre lo que les damos a nuestros hijos!

Slow food: un nuevo paradigma en la forma de alimentarse

Ayer estuve en una charla del fundador del movimiento Slow Food, Carlo Petrini, que me dió mucho que pensar. Slow Food es un movimiento que nace en 1989 en París, en oposición al Fast Food o comida rápida. Reivindica un nuevo concepto de gastronomía, más multidisciplinar, que considera los alimentos no sólo como algo lúdico o social, sino desde la perspectiva de la física, la química, la biología, la agronomía (cómo se producen los alimentos), la genética, la historia, la antropología, la cultura, la economía, etc.

Carlo Petrini, fundador del movimiento Slow Food, considerado por la revista Time como una de las 50 personas más influyentes del mundo.

En su charla, Carlo recalcó varias veces que tenemos un sistema alimentario "criminal" (dicho con sus propias palabras), pero también nos recordó que nosotros somos responsables directos de ello. Planteó nuestro papel no como consumidores pasivos, sino como co-productores, en dónde nuestro consumo influye directamente en los sistemas de producción y condiciona el tipo de agricultura. También enfatizó el hecho de que nos encontramos en una crisis entrópica, como consecuencia principalmente de que nos cuesta mucho más producir los alimentos que la energía derivada de los propios alimentos. Por ejemplo, producir un 1 kg de carne cuesta aproximadamente 5,000 lts de agua, además de una gran inversión energética como consecuencia de la dependencia en combustibles fósiles que tienen los actuales sistemas de producción: el grano para alimentar el ganado viene normalmente de otras partes del mundo, los fertilizantes necesarios para producir este grano también vienen de otros países, y todo este movimiento se traduce en consumo de combustibles fósiles (ver también esta otra entrada).

Los sistemas de producción de alimentos no son sostenibles en la actualidad por diversos motivos:

1. Agotan la fertilidad del suelo.
2. Agotan los recursos hídricos. Recordemos que el 72% del agua dulce en el mundo se destina a agricultura. Estos usos también condicionan la calidad del agua residual, que en muchas partes del mundo está contaminada.
3. Producen pérdida de biodiversidad. La selección de variedades, razas y especies más productivas en agricultura y ganadería ha motivado la desaparición del 70% de éstas durante el último siglo.
4. Promueven la desaparición del campesinado, lo que implica en muchas ocasiones una pérdida cultural de gran importancia.
   

Los defensores de los sistemas de producción de alimentos que tenemos en la actualidad arguyen que no es posible mantener alimentada a la población mundial bajo otros esquemas productivos no intensivos. Sin embargo, los datos que arroja la FAO a este respecto son muy claros:

• A nivel mundial se producen alimentos para alimentar a 12 mil millones de personas.
• Hay actualmente cerca de 7 mil millones de personas en nuestro planeta.
• 1 mil millones de personas sufren de desnutrición.
• 1.7 mil millones de personas sufren obesidad.
• El 40% de la producción alimentaria acaba en la basura.

Todo ello implica que tenemos un sistema de producción de alimentos altamente ineficiente, que genera excedentes que acaban en la basura, que consume más energía que la que proporcionan los propios alimentos que se producen, y en dónde siguen existiendo grandes desigualdades en la distribución y acceso a los alimentos.

¿Podemos hacer algo? Claro que sí. Como decía Carlo, somos corresponsables de lo que ocurre, y está en nuestra mano cambiarlo. Slow Food nace con esa filosofía y hoy son más de 100,000 personas las que se han unido a este movimiento en todo el mundo. Para más información, vísita la página del proyecto.

Software libre y evolución

¿Qué tiene que ver el software libre con la evolución? Pues mucho. Mientras que el software privativo va creciendo en función de las decisiones tomadas por un grupo reducido de personas (dirigido, eso sí, en parte por las demandas de los usuarios), el software libre va siendo construido por los propios usuarios en función de sus necesidades. Aquellas herramientas que son más útiles para otros usuarios van a permanecer y mejorarse a merced de los cambios efectuados por otros usuarios, mientras que aquello que no se use va a acabar desapareciendo... ¡toda una muestra del poder de la evolución!

En esta línea argumental se mueve el artículo de Tufto & Cavallini titulado "Should wildlife biologists use free software?", publicado en la revista Wildlife Biology en 2005. Todo un alegato al uso de software libre. Y eso, añadiré, que muchas de las herramientas que se mencionan en este artículo, incluyendo el sistema operativo Linux o los software OpenOffice, R, GRASS y Quantum GIS, han mejorado enormemente en los últimos cinco años.

Pues eso ¡viva el software libre!

Tufto, J., & Cavallini, P. (2005). Should wildlife biologists use free software? Wildlife Biology, 11 (1), 67-76 DOI: 10.2981/0909-6396(2005)11[67:SWBUFS]2.0.CO;2

Manual de comunicación para investigadores

Aquí va un vínculo muy interesante sobre como divulgar la ciencia, algo que , por desgracia, pocos científicos saben hacer bien (entre los que me incluyo). Aquí va un extracto:

"... la divulgación científica no sólo se hace desde los medios de comunicación. Se realiza también desde los museos o a través de libros y conferencias, y suele incluir la participación más o menos directa del científico. Centrándonos únicamente en la divulgación hecha desde los medios, podemos encontrar productos eminentemente divulgativos (revistas, suplementos de la prensa escrita, programas de radio y televisión) o noticias científicas mezcladas con un punto de divulgación, que se considera necesaria para entender algo mejor. En ocasiones la divulgación profundiza, otras pone en contexto, algo que es vital para hacer entender muchos temas. Muchas veces, ya que en ciencia se trabaja casi siempre desde la extrema especialización, el periodismo científico desempeña precisamente ese papel de proporcionar una visión de conjunto que la audiencia pueda digerir. En general, la divulgación también tiene mayor afán didáctico y suele ser más atemporal. Y no olvidemos que, si queremos hablar con la sociedad, deberemos ser capaces de entretener al lector, conseguir que se quede con nosotros hasta el final."

Se puede leer más en http://comunicaciencia.unirioja.es/.

Más sobre fumigaciones aéreas y procesionaria

Nuestro artículo publicado recientemente en Forest Ecology and Management sobre la inutilidad de las fumigaciones aéreas para el control de la procesionaria ha suscitado algunas críticas. La principal crítica (reiterada por el revisor de otro artículo que tenemos actualmente en revisión en Climatic Change utilizando esta misma base de datos) se refiere al hecho de que nuestro artículo sólo se refiere a rodales que sufren un grado de infestación de procesionaria alta (nivel 3 o superior sobre una escala de 5). En estos casos es lógico pensar que la plaga ya está al borde del colapso poblacional y, que por tanto, los rodales fumigados van a tener una respuesta similar a los no fumigados: esto es, un colapso da las poblaciones de procesionaria al siguiente año (se puede encontrar una explicación más detallada en esta otra entrada). Sin embargo, puede haber rodales que tengan un grado de infestación medio (por ejemplo 2) y que también sean fumigados. Se podría pensar que en estos rodales la respuesta no es la misma, y que mientras que en los fumigados se rompería el ciclo poblacional, los no fumigados tendrían más probabilidades de sufrir una superpoblación al siguiente año.

Explicaré a continuación qué parte de esta crítica tiene sustento y qué parte no la tiene. Cuando comenzamos este trabajo, tomamos la información de la Consejería de Medio Ambiente de la Junta de Andalucía. En las propias directrices de actuación de la Junta se establecía que sólo los rodales con un nivel de infestación de 3 o más son tratados, mientras que los que sufrían un nivel 2 sólo eran tratados si estaban próximos a un rodal con un grado de infestación de 3 o más. Esta información está disponible en el siguiente enlace (ver páginas 58 a 64). Como esta era información oficial, la dimos por válida sin cuestionarla. Más tarde, cuando surgieron las críticas, procedimos a verificar que, efectivamente, se fumigaban mayoritariamente rodales con un grado de infestación de 3 o más. La siguiente tabla muestra, para el período 2002-2005 (que es aquel para el que disponemos de la información más completa), el número de rodales fumigados (Trat.) y sin fumigar.

	>=3		2		1		0		Total
	Trat.	Sin	Trat.	Sin	Trat.	Sin	Trat.	Sin	Trat.	Sin
2002	47	271	23	414	44	985	29	1550	149	4240
2003	29	371	30	629	38	1074	36	1404	135	4254
2004	29	409	22	482	23	1010	39	1666	118	4271
2005	34	184	16	361	28	919	31	2132	111	4278

A partir de estos valores podemos calcular la odds ratio de la prevalencia de rodales tratados frente a no tratados para cada año entre las categorías de daño 3 o más y el resto. Para ello, haríamos el siguiente cálculo (como ejemplo tomaremos las categorías 3 o más y 2):

A = Rodales daño >= 3 Trat. / Rodales daño >= 3 Sin

B = Rodales daño = 2 Trat. / Rodales daño = 2 Sin

Odds ratio = A / B

Un valor positivo de la odds ratio indicaría que la presencia de tratamientos en rodales con un nivel daño de 3 o más ocurre con ese valor más frecuentemente que en rodales con un nivel de daño de 2. Por ejemplo, una odds ratio de 5 indicaría que los rodales con daño 3 o más se tratan 5 veces más frecuentemente que los rodales con daño 2. Hacemos estos cálculos comparando el nivel de daño de 3 o más con el resto. Los resultados se muestran a continuación.

	OR >=3 / 2	OR >=3 / 1	OR >=3 / 0
2002	3.12	3.88	9.26
2003	1.63	2.21	3.04
2004	1.55	3.11	3.03
2005	4.17	6.06	12.71

De todo esto se deduce lo siguiente. Primero, no todos los rodales que sufren un nivel de daño alto son tratados, como decíamos en nuestro trabajo. Sólo un porcentaje relativamente pequeño como vemos en la primera tabla. Esto es tranquilizador en parte, porque como hemos demostrado en nuestro trabajo, las fumigaciones producen exactamente los mismos resultados que el no hacer nada (la razón es que el propio insecto es controlado por la escasez de recursos alimenticios y el aumento de predadores y parasitoides). Segundo, es cierto que los rodales con un nivel de daño intenso son tratados con mayor frecuencia que los rodales que tienen un nivel de daño medio o incluso bajo, pero resulta curioso ver qué todavía hay muchos rodales con niveles de daño bajo que son tratados ¿qué criterios -más allá de la proximidad a rodales con un grado de infestación alto- utilizan los técnicos para decidir que estos rodales merecen ser tratados? Por último, alguien podría pensar que esto podría invalidar los resultados de nuestro trabajo, pero hemos repetido los análisis publicados en el artículo de Forest Ecology and Management, utilizando sólamente los rodales con un nivel de daño 2. Los resultados, que no muestro aquí por brevedad, muestran claramente que tampoco hay diferencias en la respuesta cuando comparamos rodales fumigados y no fumigados con un nivel de daño moderado. Por tanto, las conclusiones de nuestro estudio siguen siendo válidas.

Un festín de orugas

La procesionaria del pino (Thaumetopoea pityocampa) es un lepidóptero típico de la región Mediterránea. La mariposa de la procesionaria se aparea en verano. La hembra pone sus huevos sobre las copas de los árboles y 30 ó 40 días después nacen las orugas, generalmente en los meses de agosto y septiembre, que construyen sus nidos sobre las ramas y pasan el invierno en ellos. Entre febrero y abril descienden al suelo, forman las características filas indias –de ahí su nombre común de “procesionaria”– y se entierran finalmente en el suelo, donde pasan a la fase de crisálida. En verano las crisálidas eclosionan y surgen las mariposas, que se aparean y reinician de nuevo el ciclo. Durante el invierno, las orugas se alimentan de las hojas de los pinos en los que construyen sus nidos y esa es precisamente la causa de la defoliación.


A pesar de su toxicidad, existen varias especies de aves que han desarrollado mecanismos y estrategias para poder alimentarse de las larvas de procesionaria. Así, por ejemplo, el críalo europeo (Clamator glandorius) y el cuco (Cuculus canorus) son capaces de regurgitar los pelos urticantes de las orugas. El herrerillo capuchino (Lophophanes cristatus) y el carbonero común (Parus major) y garrapino (P. ater) no son capaces de ingerir la oruga entera, sino que las pelan como pipas, quitándoles la cabeza y el tegumento para alimentarse solamente de la parte carnosa de la larva. Estos últimos son los principales responsables de los agujeros que vemos en los nidos de la procesionaria. Existen otras especies que se alimentan de la procesionaria, pero no durante la fase de oruga, como la abubilla (Upupa epops; ver foto más abajo) que desentierra las crisálidas del suelo, o el chotacabras gris (Caprimulgus europaeus), que es capaz de cazar a la mariposa al vuelo durante su efímera existencia (generalmente no más de 24 horas).


Todas estas especies actúan como agentes efectivos para el control natural de este insecto, evitando así con su presencia la aparición de superpoblaciones de procesionaria en los pinares mediterráneos.

Barbaro, L., & Battisti, A. (2011). Birds as predators of the pine processionary moth (Lepidoptera: Notodontidae) Biological Control, 56, 107-114 : doi:10.1016/j.biocontrol.2010.10.009

Como simular un bosque en 3D

Ahora que estoy trabajando con datos espaciales de infestación de pinos por procesionaria y muérdago, estaba buscando la mejor manera de representar los datos gráficamente. Tradicionalmente estos datos se representan en superficies de dos dimensiones, pero ¿se pueden representar de una forma eficiente en 3D? La respuesta es sí y la solución nos la da (posiblemente es sólo una de las muchas soluciones) el paquete scatterplot3d de R y la función con el mismo nombre.

Veamos unos datos que simulan los datos con los que yo estoy trabajando. Coordenadas x e y con la posición espacial de los datos. Una variable z con información de la altura de los datos. Y finalmente, una cuarta variable con información sobre, por ejemplo, el número de bolsones de procesionaria (pero podría ser cualquier otra cosa).

x <- rep(1:10, each=10) + rnorm(100, 0, 0.2)
y <- rep(1:10, 10) + rnorm(100, 0, 0.2)
z <- rnorm(100, 6, 1)
procesionaria <- rpois(100, lambda = 5)
procesionaria.col <- cut(procesionaria, breaks=c(0, 5, 10, 50, 100), labels=c("greenyellow", "green2", "forestgreen", "darkgreen"))
table(procesionaria.col)

library(scatterplot3d)
scatterplot3d(x = x, y = y, z = z, type="h", cex.symbols=5, pch=19, color=procesionaria.col, xlab="", ylab="", zlab="Altura", zlim=c(0,10))

Created by Pretty R at inside-R.org

Y el resultado sería este: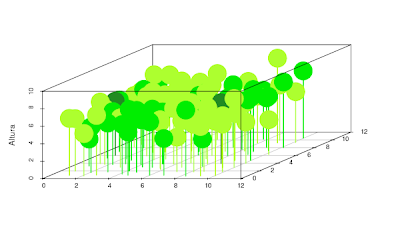

Modificando los argumentos de la función scatterplot3d() podemos hacer que el color de los árboles sea representativo del grado de infestación por procesionaria (más oscuro más infestado). También podríamos, si quisiéramos, hacer que el símbolo de copa representara la especie.

Por cierto, gracias Antonio por enseñarme Pretty R para incorporar código de R en mis entradas. ¡Con todo el tiempo que llevo en ésto y todavía no lo conocía!